原始题目：剑指 Offer 30. 包含min函数的栈 (opens new window)

解题思路：

可以借助辅助栈，用来保存当前主栈中的最小值，具体如下：

首先有两个栈 $S1$ 和 $S2$，$S1$负责存储压入和弹出所有元素，$S2$ 负责保存当前元素中的最小值。下面通过一个例子来说明，也可以直接看结论。

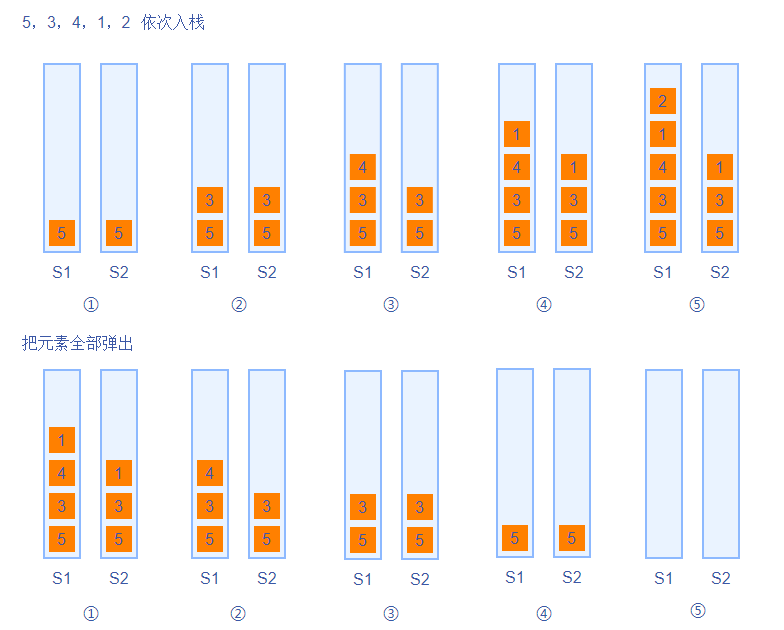
压入阶段

1. $5$ 压入的时候，$S1$ 正常压入，因为当前 $S2$ 是空的，所以 $5$ 压入 $S2$ 中；
2. $3$ 压入的时候，$S1$ 正常压入，因为当前 $S2$ 的栈顶元素 $5$ 大于 $3$，所以 $3$ 压入 $S2$；
3. $4$ 压入的时候，$S1$ 正常压入，因为当前 $S2$ 的栈顶元素 $3$ 小于 $3$，所以 $4$ 不压入 $S2$；
4. $1$ 压入的时候，$S1$ 正常压入，因为当前 $S2$ 的栈顶元素 $3$ 大于 $1$，所以 $1$ 压入 $S2$；
5. $2$ 压入的时候，$S1$ 正常压入，因为当前 $S2$ 的栈顶元素 $1$ 小于 $2$，所以 $2$ 不压入 $S2$；

弹出阶段

1. 当 $2$ 弹出时，$S1$ 正常弹出，因为当前 $S2$ 的栈顶元素 $1$ 不等于 $2$，所以 $S2$ 不弹出；
2. 当 $1$ 弹出时，$S1$ 正常弹出，因为当前 $S2$ 的栈顶元素 $1$ 等于 $1$，所以 $S2$ 弹出；
3. 当 $4$ 弹出时，$S1$ 正常弹出，因为当前 $S2$ 的栈顶元素 $3$ 不等于 $4$，所以 $S2$ 不弹出；
4. 当 $3$ 弹出时，$S1$ 正常弹出，因为当前 $S2$ 的栈顶元素 $3$ 等于 $3$，所以 $S2$ 弹出；
5. 当 $5$ 弹出时，$S1$ 正常弹出，因为当前 $S2$ 的栈顶元素 $5$ 等于 $5$，所以 $S2$ 弹出；

总结

• 压入元素 $x$ 时，$S1$ 都是正常压入，而 $S2$ 则需要判断当前的栈顶元素 $a$ 是否大于等于 $x$，如果大于 $x$，说明此时 $a $已经不是最小的了，把 $x$ 压入 $S2$；否则不压入 $S2$。

  • 为什么是大于等于？

    如果连续压入两个最小元素，比如压入两个 $0$，那么 $S2$ 也要压入两次 $0$，这是因为弹出时，是通过判断 $S1$ 和 $S2 $ 栈顶元素是否相等来决定是否要弹出 $S2$ 的。因此在 $a = x$ 的时候，也要将 $x$ 压入 $S2$。

• 弹出元素 $x$ 时，$S1$ 都是正常弹出，而 $S2$ 则需要判断当前的栈顶元素 $a$ 是否等于 $x$，如果等于，说明 $a$ 是在$x$ 压入时，一起压入 $S2$ 的，需要把 $a$ 弹出。否则不弹出 $S2$ 栈顶元素

代码：

class MinStack {
    /**
     * mainStack 存放着所有的元素
     */
    private final Deque<Integer> mainStack;
    /**
     * minStack 的栈顶存放着 mainStack 中的最小值
     */
    private final Deque<Integer> minStack;

    /**
     * initialize your data structure here.
     */
    public MinStack() {
        mainStack = new LinkedList<>();
        minStack = new LinkedList<>();
    }

    public void push(int x) {
        mainStack.push(x);
        if (minStack.isEmpty() || minStack.peek() >= x) {
            minStack.push(x);
        }
    }

    public void pop() {
        // 如果弹出的不是最小值，那么 minStack 就不用动
        // 如果弹出的是最小值，那么 minStack 只需要把栈顶弹出即可
        if (mainStack.pop().equals(minStack.peek())) {
            minStack.pop();
        }
    }

    public int top() {
        return mainStack.isEmpty() ? -1 : mainStack.peek();
    }

    public int min() {
        return minStack.isEmpty() ? -1 : minStack.peek();
    }
}

复杂度分析

• 时间复杂度$O(1)$：push(), pop(), top(), min() 四个函数的时间复杂度均为常数级别。
• 空间复杂度$O(N)$：当共有 $N$ 个待入栈元素时，辅助栈 $S2$ 最差情况下存储 $N$ 个元素，使用 $O(N)$ 额外空间。